트레이더들을 위한 시계열데이터 처리, Learning Representations for Time Series Clustering
안녕하세요
예전에 Auto Encoder를 통해서 시계열데이터를 압축된 벡터 데이터로 변환하는 로직에 대해 설명드렸고
오늘은 그것을 트레이딩에 활용할 수 있는 방안들에 대해 이야기를 할 예정입니다.
오늘 글 내용은 NIPS DSBA 연구실의 Paper Review를 많이 참고하였습니다.
제가 늘 좋은 내용의 리뷰와 인사이트를 얻는 곳이기도 합니다.
Representation Learning
Representation Learning은 데이터로부터 의미 있는 표현을 학습하는 과정입니다.
데이터의 복잡한 구조와 패턴을 캡처하고 이해하기 위해 사용됩니다.
Representation은 데이터의 복잡한 구조와 패턴을 캡처하고 이해하기 위해 사용됩니다.
이런 표현은 보통 고차원의 데이터를 저차원의 벡터로 변환하거나
자연적 데이터를 기계가 이해하기 쉬운 형태로 바꾸는 데 사용되기도 합니다.
Representation Learning을 학습해 둔다면
자주 접하는 원천 데이터에 대해 자동화된 특성을 추출할 수 있습니다.
Trading AI는 차트데이터를 평생 입력으로 받으며 작동합니다.
시간이 지날수록 받아들이는 차트데이터는 많아질 것이고
많은 양의 고차원의 데이터를 보면서 불필요한 부분은 무시하거나
차트에서 주는 의미 있는 부분만 캡처해 내서 압축된 형태의 특성을 만들어낼 수 있습니다.
이 부분은 지난번 시간에서 Feature Engineering을 Auto Encoder를 통해 수행한 것과 유사한 맥락입니다.

차트데이터
제가 인공지능을 통해서 트레이딩을 해보기 전에
서점에서 어떤 책을 본 적 있습니다.
극강의 T인 제가 보기에는 도저히 납득할 수 없는 내용이었습니다.
차트데이터가 어떤 패턴으로 흘러가는지 이런 패턴에선 어떻게 동작한다 식의 내용이었습니다.
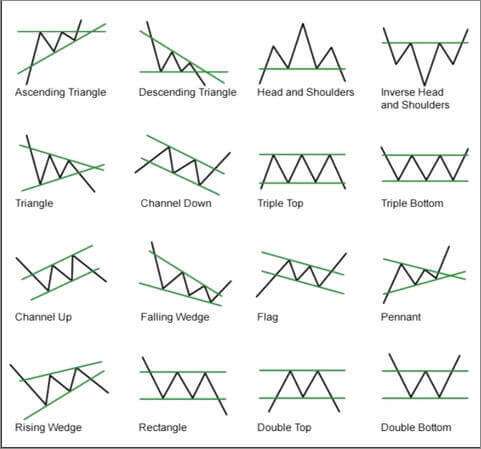
사실 지금은 이런 패턴들이 어느 정도 의미 있다고 생각합니다.
실제로 시장이 이런 움직임을 보이는 이유는
시장을 이루는 것들은 시장참여자, 사람들이고
많은 사람들이 저런 패턴데이터에 반응하는 군집을 이룬다면
실제로 데이터는 저렇게 움직이고 처음엔 논리와 근거 없이 설명한 이론들이 맞는 설명이 되게 됩니다.
시장을 만들어가는 건 시장참여자들의 심리입니다.
아무튼 위에 예시처럼 사람이 트레이딩을 할 때 차트를 보면서 위와 같이 패턴을 외우고 행동하곤 합니다
전달된 차트데이터를 보면서 패턴을 적용하거나 학습된 패턴에 따라 어떻게 행동할지 이어지는 것처럼
인공지능 모델들도 전달된 차트데이터에 패턴을 적용하기 위해
데이터를 어떤 패턴이다라고 정의하고나 분류할 수 있어야 합니다.
사실 시계열데이터의 분류 작업은 Supervised learning입니다.
즉, 트레이딩 데이터를 보고 정해둔 기준에 따라 분류하는 모델을 만들려면
시계열데이터에 정답지인 라벨데이터가 있어야 하고 이를 데이터셋으로 모델을 학습시켜야 한다는 것입니다.
물론 자연적으로 발생하는 시계열데이터에 라벨 데이터를 부여하는 작업을 수행할 수 있지만
그런 라벨데이터는 트레이딩 영역에선 주관적이기도 합니다.
시계열을 어느 정도로 보느냐에 따라, 기대수익을 어느 정도로 설정하느냐에 따라
수익인 구간과 손실인 구간이 동시에 발생할 수 있기 때문입니다.
그래서 결국 제가 원하는 방향은 모델이 스스로 데이터의 라벨링을 할 줄 알아야 한다고 생각합니다.
그래서 Unsupervised Learning Clustering을 이용할 생각입니다.
Clustering
입력된 트레이딩 영역의 시계열데이터, 즉 차트 데이터를 보고
특정 기간으로 segment를 나누어 라벨링을 진행할 예정입니다.
가격 데이터가 유의미하게 움직이는 순간을 포착해서 segment를 나누면 더 좋겠지만
이건 추후 고도화 과정에서 진행해 볼 예정입니다.
시계열데이터를 Clustering 한다면 어떤 점들이 좋을까요
저는 Clustering 해서 모델이 만들어낸 고유한 벡터나 라벨들을 활용해서 데이터 분석을 진행할 예정입니다.

위 예시는 RNA 분자 안에서 염기의 연속적 순서를 보여주고 있습니다.
DNA는 A, C, G, T의 네 가지 염기로 구성되며, RNA는 A, C, G, U로 구성됩니다.
이 서열은 생물학적 정보를 나타내며, DNA의 경우 생명체의 기능을 지시하는 중요한 정보를 담고 있습니다.
각 핵산은 포스페이트 그룹, 설탕(리보오스 또는 디옥시리보오스), 그리고 염기로 구성된 뉴클레오타이드 연쇄로 이루어져 있습니다.
핵산 서열은 단백질 합성에 필요한 아미노산의 순서로 번역되며, 각 코돈이라 불리는 세 개의 염기가 하나의 아미노산에 해당합니다.
위 예시처럼
우리가 Clustering을 통해 시계열데이터들에 라벨들을 찾아 나열해 보면
시계열데이터들의 segment 조합들을 얻을 수 있습니다.
예를 들어 A, B, C,.. Z로 클러스터링 된 Encoder를 완성했을 때
A, Z, C -> F가 올 확률 분포, B, V, W -> H가 올 확률 분포를 알 수 있게 됩니다.
이렇게 된다면 제가 예전에 책에서 읽었던 여러 차트패턴들에 대해
통계학적인 근거를 기반으로 트레이더들에게 유의미한 정보로 제공될 수 있을 거라고 생각하고 있습니다.
Paper Review
DSBA연구실의 Paper Review 발표자료에서 아래와 같이 잘 설명된 한 장의 그림을 보겠습니다.

DTCR 이라고도 불리는 논문의 리뷰 내용을 대략적으로 설명하자면
입력된 데이터들을 잘 압축해서 설명하는 Encoder(Representation Model)를 만드는 과정을 진행합니다.
이 부분이 Pretext Task가 되고, 이후 Clustering Task를 진행하면서 이 Representation Model을 사용할 예정이기 때문에
애초에 Pretext Task과정에서 Representation Model을 학습할 때 Object Function 자체를
Clustering을 위해 설정해 두는 개념입니다.
Representation 자체가 고차원 데이터를 압축하다 보니 일부 표현의 손실이 발생합니다.
이때 우선적으로 중점을 두는 곳을 설정해 두어서 Representation을 내가 원하는 바대로 표현하는 것을 중점을 둔다는 것입니다.
Clustering에 적합한 Objective Function은
Spectral Relaxation for K-means Clustering (NeurIPS 2001)에서 얻을 수 있습니다.
Spectral Relaxation for K-means Clustering에서
기존의 K-means Clustering에서는 sum-of-squares를 minimization 하는 것을 목적으로 두고 있었습니다.

위 예시에서 cluster 내부 벡터들 간에 sum-of-squares들의 합이 적을수록
잘 나눠진 cluster model인 것을 알 수 있습니다.
Spectral Relaxation은 행렬의 연산을 통해서 K-means clustering의 sum-of-squares minimization 식을
Gram matrix를 활용하여 trace Maximization으로 재정의할 수 있습니다.
trace maximization문제의 relaxed version은 Gram matrix의 partial eigen decomposition을 통해
계산되는 global optimal soulution을 가지고 있음을 증명합니다.
Deep Temporal Clustering Representation (DTCR)

Encoder
시계열데이터에 대해 입력을 받아서 Temporal Dynamics, Multi Scale Characteristics를 추출하기 위해
Multi Layer Dilated RNN 구조를 사용합니다.

입력된 시계열에 대해 정해진 주기(1, 2, 5,... 등)로 RNN계층을 설정합니다.
이렇게 되면 조밀하게 데이터를 보는 계층도 있고
좀 더 듬성듬성 데이터를 훑어보면서 큰 타임스텝으로 데이터를 살펴볼 수 있게 됩니다.
마지막에는 각 계층을 concat 하여 representation으로 도출해 냅니다.
Reconstruction
Auto-Encoder에서 설명했던 것처럼,
Encoder를 통해 Representation vector를 만들고 reconstruction 원복작업을 거쳐 Representation에 대한 학습을 합니다.
Representation들에 대한 K-Means Loss를 설정해 두면 이제 Encoder가 시계열데이터에 대한 Cluster vector들을 만들어내고
이 vector들을 Decoder에 입력으로, 다시 원본 데이터로 잘 Reconstruction 할 수 있도록 설정합니다.
Classification
입력된 시계열을 랜덤 하게 shuffle 하여 Encoder에 넣고 나온 결과에 대해 Binary Classification을 통해
가짜임을 잘 판별해 내는 Classification을 설정합니다.
Encoder가 차원을 축소하고 함축적인 Representation을 하다 보니 거짓된, 혹은 노이즈데이터로만 입력되어도
유의미한 데이터벡터로 산출될 수 있는 경우를 방지하기 위해 가짜 샘플데이터에 대한 분류를 잘 해내도록
Encoder에 대한 제약조건이 추가된다고 보면 될 것 같습니다.
논문에서 제안하는 구조에 대한 설명은 마쳤습니다.
원래는 일부 트레이딩에 자주 사용되는 섹터나 ETF, 지수들에 대해
학습을 하고 분류된 결과를 공유하려고 했는데 시계열 모델을 official code를 살펴보니
Tensor flow 1.x 대 버전으로 작성되어 있었습니다.
제 GPU 환경이 2.0 이상의 Tensor flow만 구동가능해서
결국 일부 트레이딩에 맞게 변경도 할 겸 변환하는 작업을 진행하고 있습니다.
실제 논문을 어떻게 활용할지에 대해서는 직접 구현을 해보고
Tensor flow.js를 통해 웹에 배포해서 많은 분들이 참고할 수 있도록 공개할 예정입니다.
마무리로 정리를 해보자면
저는 트레이더들, 투자자들 시장에 참여하는 여러 사람들에게
의사결정을 위해 이 금융 도메인에 속해있는 사람들에게
의미 있는 정보를 제공하기 위해 노력하고 있습니다.
그 긴 여정 중 현재는 시계열데이터에 대한 Clustering 모델을 만들기 위한 연구과정을 보여드리고 있습니다.
시장을 분석하는 여러 유형의 사람들이 있지만
제가 좋아하고 잘하는 것들을 통해 많은 분들에게 의미 있는 가치를 줄 수 있으면 좋을 것 같습니다.
연말 잘 보내시고
오늘도 감사합니다.